わくわく授業のアイデア
このコーナーでは、生徒の意欲を高めるために先生方が授業のなかで工夫しているちょっとしたコツを紹介します。
|
| ●学習意欲を高める算数の授業のコツ |
| 算数は得意だったのに、中学で数学になった途端に成績が急降下する…。そういう子どもは少なくない。数式の持つ意味を理解せず、訓練中心の学習を続けていたからだ。数学のみならず、他教科でも必須となる論理的思考力。盛永先生は算数の授業を通し、この「解く力、解く喜び」を着実に身につけさせている。 |
| まず、児童にオリジナルの解法をつくらせる |
「単元をこなすだけなら学校でなくてもいい」
盛永先生はこう言い切る。塾や家庭教師で代替が利くのだという。学校という環境のなかでしなければいけないこと、教師にできることは何か? 海外でも教鞭をとった経験を生かし、たどり着いたのが、問題解決型の学習によって論理的思考能力を研いていく手法だった。
盛永先生の算数は、まず児童にオリジナルの解法をつくらせることから始まる。
加減乗除、図形の面積、分数、どの単元でも、授業開始からたっぷり15分間かけ、まず課題を子ども自身に解かせる。文章での説明、数直線を使ったもの、数式や図を使うなど、なんでもいい。正答、誤答いろいろあるが、まず自分で解法を考えられたことをほめる。ここからが本番だ。 |
コツ1 ハンドサインを用い、全員参加の態勢をつくる。
わからない児童を「お客さん」にしないことで、落ちこぼれを出さないようにする |
|
「すぐに正解は発表せず、いくつか特徴のある解法をピックアップしてそれを説明させ、クラス全員にハンドサインで『意思表示』をさせるのです」
ハンドサインとは、その解法に賛成、もしくは理解した場合はジャンケンのパー、不満または別の考え方の場合はグー(パンチの意)、意味がわからず質問したい場合はチョキ。補足したい、または補足すればOKという場合は指を1本を出すというもの(図1)。全員が、なんらかのサインを出さなければならないところがミソだ。
ここで討論とともに相互啓発が生まれる。Aさんの考えのほうがいい、Bさんの考え方のほうが計算式が短くてすむ、Cさんの考えにDさんの考えを足せば…、こう授業を誘導していくことで、自分が間違っていた点や、正解にたどり着く手法が1つではないことを、子ども自身に気づかせていく。
ピックアップした解法を考えた児童に、黒板の前で説明させることが大切である。直感的に理解したつもりでも、他人に説明するとなると論理的な整理が必要になる。
また正答でも、質疑応答を交わし説明責任を果たすことで、より論理はシェイプアップされる。できる子は率先して前に出られ、より高い理解、難度の高い設問を自ら求める気持ちも生まれるという。
「しかし、チョキがなかなか出ない。わからない、質問したい、というのは言い出しにくいんでしょうね」 |

| ▲図1 ハンドサイン。盛永先生の教室前方にはこの絵が張られている。これで全員がなんらかの意思表示ができる |
|
| コツ2 単元で必要になりそうなヒントを予測して、ヒントカードを作っておく。電卓など補助ツールは用意はするが、最初から与えない |
|
だが、仲間がつくったいろいろな解法の前で逡巡しているときこそ、その子の論理力を引き出す最大のチャンスだ。ここで、「キミの解答のここまではAさんと同じだよ」また、「Bさんとはここが違うね」と指導していく。
「少人数で討論させたり、隣と相談してもいいよ、というアドバイスをすることもあります。それからヒントカードを用いることもあります」
設問を解くためのカギを記載してあるのがヒントカードだ。例えば6年生の授業で、立方体の展開図を描かせる場合、正方形を4つ並べて描いておく。正答の多くはこの図に正方形を2つ足して展開図が描けるからだ(図2)。また、盛永先生は電卓も否定しない。面積や人口密度など、計算自体が主目的ではない場面では、電卓を使いたい子どもには使わせる。
「ただ、最初から渡さない。用意だけしておきます」
あくまで子どもが電卓を使いたいと考えたなら、使えばいいというスタンスなのだ。
盛永先生のこうした工夫で、授業は子ども同士の討論が中心になっていく。
「大きな劇を創るようですよ。みんなで討論し、正答へと向かい、そこで真理に出合って感動するという」
一度、原理原則を理解すれば、それは同種の、どんな複雑な問題にでも適用できる。そこに真理があるという感動をクラス全員で共有させるのだ。
しかし全員参加の態勢をつくるには、やはり教師のリードが必要だ。子どもにとって、自分のつくった解法を全員の前で発表するというのは勇気のいる作業だからだ。
「年度初めにそうした雰囲気づくりをしなくてはならない。だからまず『間違ってもいいんだよ』『友だちが助けてくれるよ』と」
前述した、まず自分で考えられたことをほめるというステップはここにつながる。 |
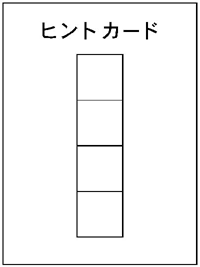
| ▲図2 問題を解く助けになるヒントカード。例えば、これを使えば立方体の展開図が簡単に描ける |
|
| ココツ3 テレビや生活のシーンから、単元につながるテーマを導入する。具体的な事例を盛り込むことで、数の持つ意味を皮膚感覚で理解させる |
|
さらに子どもの興味を引く例題も活用する。食べ物やスポーツ、時事の話題。「小数点第2位の計算の際は、長野オリンピックの男子スケートの決勝シーンのビデオを活用しました。ちょうどメダルの色が小数点第2位で入れ替わるレースでしたから」
そのほか、異分母分数の計算では透明シートに6等分と8等分にされたピザの絵を書いておき、重ね合わせて見せる。共通する目盛りを作り、まず分母をそろえないと、計算式ができないことを視覚に訴えるのだ。 |
| 「合併」と「増加」の概念 |
| 盛永先生のこうした手法は、初めて算数にふれる1年生から有効だという。例えば、整数ひとけたのたし算の文章題。 |

| 『赤いりんごが3個と、青いりんごが2個あります。全部でいくつ?』(合併) |
|

| 『子どもが3人で遊んでいます。2人が仲間に入れてとやってきました。ぜんぶで何人?』(増加) |
|
この2問を絵に描いて黒板に張っておく。(上図)
数式にすれば3+2で同じ。だが、ここには数学的思考が必要になる、合併か、増加か、という概念が隠されている。そこで同じような問題を児童につくらせ、でき上がった問題を、2つにグループ分けして張っていく。
「これとこれは同じ意味だね、と理解させるんです」
こうした意味を考えさせる訓練は、引き算が用いられる場面の違いに目を向けたり、学年が進んで集合の概念を理解させるときに役に立つ。 |