数　学
授業時間減による演習時間の減少を補うための週末課題

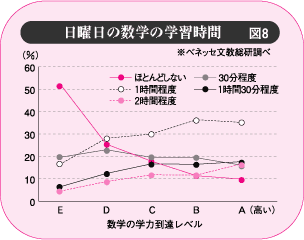
　週5日制の実施によって、数学で最も問題になると思われるのが、演習時間の減少である。図8を見ても分かるように、今回の結果においても、休日の学習時間は低学力層になるにしたがい少なくなっている。土曜日が完全に休みとなると、このような傾向が強まり、休日の学習時間の減少は、より一層深刻になることが予想される。
　到達基準を越えるために、週末課題を与えて週明けに提出させたり、週明けに小テストを行い評価機能を持たせることで、生徒を学習へ誘う工夫をしているケースが多い。しかし、これだけではなかなか効果は現れない。そこでこれに加え、提出させた課題ノートに検印だけでなく、コメントを一つ入れて、生徒のやる気を喚起するという方策を取っている高校もある。「前回できていなかったところが、正解できるようになったね」と一言入れることによって、教師が自分のことを見ていてくれるのだという意識を付けさせ、学習に向かう意欲を高めるというわけである。
　また、「数学を学ぶことの意義」を理解させることも重要だ。経済学部の先輩を呼んで、理系だけでなく文系であっても数学が必要であることを語ってもらい、数学を「学ぶ必要のあるもの」として認識させるのも一つのやり方だ。

基本問題の反復演習で徹底理解を

　では、家庭学習で扱う演習内容はどういったものにすればよいのだろうか。今回の結果から見ると、到達基準前後と達成基準前後では明らかに学力要件に差異が出ている。
　到達基準に達しないレベルでは、基本的な定理・公式の理解度が低い。つまり、この成績層の生徒は定理・公式の多さに目を奪われるあまり、一つひとつの理解が確実になっていないままに次の内容に取り掛かる傾向が強い。そのため、すべての内容があやふやになり、公式の符号の覚え間違いを起こしたり、全く別の公式を使って無理やり問題を解こうとする。このような面を修正していくためには、いたずらに発展的なレベルの問題を与えず、基本的なものを反復演習させることが重要である。
　達成基準を越えられない生徒は、定理・公式はある程度理解しているのだが、文字が入って計算が複雑になっているものや、見た目の表現が少し変わっている問題になると、一気に正答率が下がることが多い。つまり、基本的な問題でないと解けない生徒と言える。これは問題と解法を一対一で対応させて覚えようとしていることから生じている。この状況を脱しない限り、応用的な問題には歯が立たない。このような生徒については、どういう条件下で、どの解法が有効なのかを理解させるために、出題の切り口は異なるが同じ解法を扱った問題を複数解かせることによって、条件と解法を結び付けるトレーニングをさせるとよいだろう。