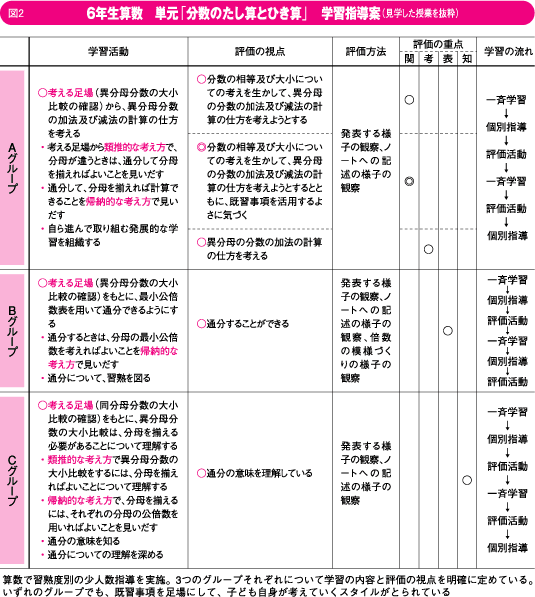
PAGE 12/18 　 「考える足場」から子どもの思考活動を促す 　桃山東小学校では、04年度から、算数に習熟度別の少人数指導を導入した。見学した６年生の単元「分数のたし算・ひき算」も、A・B・Cの三つのグループ別に授業が進められている。すべてのグループに共通するのは、冒頭で、前時までの授業のポイントが「考える種」として板書される点である。子どもたちは、これを足がかりに、新たな課題に対して推論を働かせる。 　最も理解が進んでいるAグループの課題は、異分母分数のたし算やひき算の方法を考えること。教師は「考える種」として、分母が同じ分数のたし算や、分母が異なる分数の大小比較といった解法へのヒントを板書し、異分母の分数同士のたし算に取り組ませた。続いてひき算にも挑戦させ、答えと解法を発表させた後、「たし算とひき算で、共通していることは？」と全員に問いかけた。個々の事象から一つの法則を導き出す、帰納的思考を意識した質問だ。子どもたちからは、「たし算もひき算も単位となる分数のいくつ分になるのかを考えればよい」といったポイントが導き出される。 　Bグループのこの日の目標は、分数を通分するときは、分母を最小公倍数にすることに気づくことだ。「考える種」には、分母の大きさを揃えれば異分母分数の大小比較ができることが示されている。十分に通分の練習をさせたあと、教師は、「これまでの問題に共通することは？」と、推論を促す質問を投げかけた。やがて「通分をするときは、分母の最小公倍数を見つければいい」とねらい通りの答えが返された。 　通分の意味を理解するのが目標のCグループでは、「考える種（１）」で、分母が同じ分数同士は大きさを比べやすいことを図解で示し、さらに「考える種（２）」では1/2と1/3を通分する過程を詳細に説明していた。授業では、1/2、2/4、3/6…のように、大きさの等しい異なる分数を作る練習を進め、それをもとに分数の大きさを比べる指導が丁寧に進められた。そして、全員がある程度の理解を深めた段階で、「大きさ比べをして、気づいたことはありますか」と、子どもたちの推論を促す。 　「こうした授業を繰り返すことで、初めて向き合う課題でも、既習事項（考える種）を足場にすることで、答えが導けるという意識が植えつけられていきます。さらに、自力で考えたという実感が得られ、子どもの意欲もわいてきますね」（中島校長） ▼クリックすると拡大します。 Aグループの授業の板書 Bグループの授業の板書 Cグループの授業の板書 　　PAGE 12/18