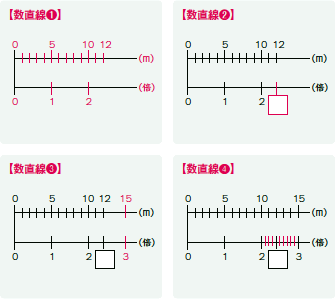
PAGE 13/21 　 時間 場面 授業の展開 中村先生の視点 48分 　 ＊図の赤字は１～４の各段階でかき加えられた部分 Ｄくん「２倍から３倍まで５マスしかないから、１マスが0.2倍になる。0.2倍が２つだから0.4になる」 T「どういうことか分かる？　 １マスが0.2で、５マスで１増えている。その２つ分で0.4じゃないかということだね。１マスが0.2というのを、もう少し分かりやすく目盛りを工夫出来る人はいないかな？」 Fさん　数直線に記入【数直線４】 T「Fさんが何をしたか分かった人？　言葉で説明出来る人はいる？」 Eさん「0.2を0.1のところで切った」 T「つまり、Ｆさんは２から３の目盛りを細かくして10等分にしたということだね。すると、Ｄくんが□にしたのはいくつ目になる？」 Gくん「４つ目」 T「ということは、0.1の４つ分で0.4。だから２から0.4増えて、□は2.4ということが分かりそうだね。式の結果と数直線で考えたものが同じになったね。これからは数直線が使えそうかな。テープ図で迷っていた人もいたようだから、次の時間にやってみよう」 佐藤先生のねらい　方眼の0.2単位のマスを使って2.4がすぐに導き出されることは予測していた。更に小数への理解を深めさせるため、10等分させて0.1単位で考えさせたかったが、なかなか出てこなかった ↓クリックすると拡大します 　 　2.4倍を子どもにとらえさせる方法は、二つあった。 　一つは、0.2を単位とする方眼に目が向いてしまい、１０等分する発想が出てこなかったので、黒板に直接数直線をかいて、方眼を使わずに、数直線のみで考えさせる方法。目測で「2.4」「2.5」などを示すうちに、正確な位置を出すために１０等分の発想が出てくるだろう。 　二つ目は、授業ではあまり注目されなかったＡくんの発言（比較検討２の★）をここで取り上げ、「数直線上で表すと、どうなる？」と聞く方法。Ａくんは１０等分の発想を持っていたはずである 53分 57分 まとめ T「今まで出た考えとか、迷ったこと、迷いがすっきりしたのであればどこですっきりしたのかなど、授業の流れを思い出しながら学習の感想を書いてください。友だちのアイデアについても書いてくださいね」 ある児童の学習感想 「私は位分けが思いつかなかったから、Ｄくんのやり方を見て、なるほどと思った。私はテープ図をかいているとき少しまよってしまったけど、ＤくんやＦちゃんのようにやれば答えが出ることがわかった。Ａくんの説明で2.4はどんな数かということがわかった」 既習内容なので、全員で方法を確認する必要はなかったのではないか。それぞれの子どもに任せれば、時間を３分間程短縮出来た 　　　PAGE 13/21