数学的な見方・考え方を育む授業とは？ （話題提供：立命館宇治中学・高等学校 酒井淳平）

「生徒の気づきと学びを最大化するプロジェクト」第114回
「数学を学ぶ意味を見つめ直し、これからの数学教育を考える」開催

ベネッセ教育総合研究所では、有志の教員らがオンラインで対話する「生徒の気づきと学びを最大化するプロジェクト」を、2020年4月から週１回のペースで実施している。2022年9月の第114回では、数学の学びのあり方をテーマに対話会を行った。全国から参加した小学校・中学校・高校の教員や、教育関係者らが、担当教科や立場を超えて議論を深めた。

何のために数学を学ぶのか？

対話会の冒頭では、話題提供者である立命館宇治中学・高等学校の酒井淳平先生が、現在の数学教育についての問題意識を語った。

まず、「数学は、社会の役に立つのか」という問いに対し、酒井先生は、数学者が数学を探究する姿勢を通じて説明。「数学者は、そこにある問題を解きたい、何かを明らかにしたいといった純粋な思いで探究していきますが、その結果は社会の役に立っています。例えば、数百年間にもわたったフェルマーの最終定理を解く過程では、整数論が発達し、暗号化技術につながりました。社会の役に立つのは結果であり、目的ではない。それが、数学だと考えています」と意見を述べた。

生徒に数学を学ぶ意味を説明する際にも、「頭を鍛えられる」「抽象的な理解力がつく」「課題解決力がつく」といった社会で求められる力が身につくことに加えて、「数学は、世界共通のグローバルな言語であり、数学者の夢に触れられて、結果的に社会の役に立つ」と伝え、数学の本質を理解するように促しているという。

問題を解くことに終わらない算数・数学の学びを目指して

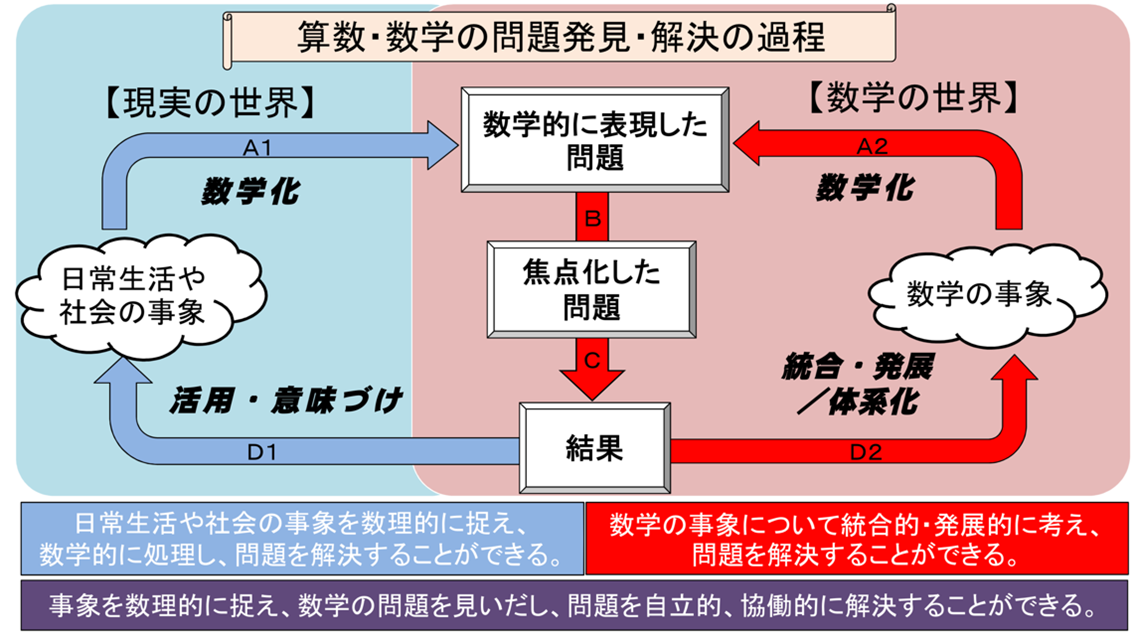
続いて、酒井先生は、「算数・数学の学習過程のイメージ」（図）を提示し、数学的活動のサイクルを回すことの重要性を説明した。「現在の数学の授業では、数学の問題を解くことに終始していますが（図のC）、それは、数学の学びのごく一部に過ぎません。数学的活動を通じて、数学的な見方・考え方を働かせて、数学的に思考する力を育むことこそが、数学の学びです。その力がつくと、物事を見る際の幅が明らかに広がります」と述べた。

そして、数学的な見方・考え方を働かせる学びを実現するためには、授業改善によって学びの質を高めることが大切だと語った。「どの教科にも言えることですが、受験勉強のために学んだ知識は忘れてしまいがちです。数学でも、公式に数字を当てはめて問題を解くだけの学習では、様々な場面で活用できる知識・技能はほとんど身につかないでしょう。生徒が数学的活動に取り組み、数学的な見方・考え方を育てる授業にすることが必要だと考えます」と考えを示した。

プロセスを重視した学びへの転換を

話題提供の締めくくりとして、文系の数学を含めて、高校数学のあり方を再検討する時期が来ていると、酒井先生は課題意識を示した。「文系の生徒も数学的な見方・考え方を身につけることが大切にもかかわらず、現状では、大学入試のために学ぶことが中心になりがちです。教えられた解法を真似して、いかに早く、正確に解くかではなく、解法を知るプロセスにもっと重点を置くべきではないでしょうか」と指摘した。

話題提供を受け、ある小学校教員は、「小学校でも、本来は算数と理科がつながっている面白さを教えたり、問題を解く過程を重視したりする学びを大切にしたいという思いがあります。しかし、実際には、早く正確に計算を解く学習が重視されています。小学校の算数の授業が変わらないと、中学校・高校の数学も変わらないという問題意識があります」と語った。

ある高校の数学教員は、大学で初めて数学の面白さを知り、中学・高校で学んだ数学への理解が深まったという自身の経験を語った上で、「そもそも数学は何を学ぶ教科なのか、よく理解していない生徒は多いはずです。教員は、数学の授業で学ぶこと、身につけたいことを整理して、生徒に伝える必要があり、生徒とじっくり議論した方がよいと感じました」という考えを示した。

学習内容の背景理解が大切

次に、グループに分かれて対話を深めた。

あるグループでは、「定義から発展するプロセスだけを数学と呼んでいると感じますが、それは妥当なのでしょうか」という問いかけから議論が進んだ。メンバーの１人は、「例えば、数学の授業では、虚数の定義から発展するプロセスのみを取り扱います。しかし、なぜ、どのようにして虚数が生み出されたのかまで理解できると、虚数をどこで、どう使えばよいかを考えられるはずです。そこまで学びを深めて初めて、先ほど示された算数・数学の学習過程のイメージになるのかもしれないと思いました」と語った。

文系数学のあり方に関して議論したグループもあった。ある参加者は、「『文系数学は暗記する内容が多い』と言われることがありますが、それは数学だけに限りません。歴史も暗記科目と言われやすいですが、歴史上の出来事を用いて論理的に思考したり、学者の見解を検討したり、対話をしたりすると非常に面白い学びになります。同様に、文系数学でも、授業のあり方によって、生徒は数学の学びを楽しめるはずです」と提案した。

別のグループでは、ある中学校教員が、１人の生徒が抱いた疑問をきっかけに、数学の授業について生徒同士が議論をした経験を語った。それは、二項定理の授業で、「この方法で答えが出るのは分かったが、どうしてこの式が成り立つのかが分からない」と、生徒から疑問が示された。すると、「答えが出るなら、それでいい」と主張する生徒たちと、「確かに、なぜこの式が成り立つのか分からない」と考え始めた生徒たちに二分し、議論が白熱したという。「その生徒は、とてもよい問いを提示してくれました。中学生でも、そのように疑問を掘り下げられます。最終的には、二項定理が成り立つことを理解するためには、数学的帰納法を学ばないと難しいと伝えました。その生徒とは、個別に話して、考えを深められるようにしたいと考えています」と述べた。

小学校から学びの背景にある考え方への理解を促すことで、小中の学びのギャップに対応しやすくなるのではないかといった意見も出された。

ある参加者は、「小学校の算数の授業では、子どもにとって身近な例を題材にして学びを進めますが、中学校の数学の授業は概念的になり、その違いに戸惑う生徒が多いようです。小学校の授業でも、算数の学びの背景に触れ、子どもの疑問を大切にしたり、算数の面白さを感じさせたりすることで、子どもが『今なぜそれを学ぶか』を理解しながら学べるようになるのではないでしょうか」と語った。

総合数学力への違和感

グループでの対話を終え、酒井先生は、「今日は数学がテーマでしたが、他教科の先生との対話は大事だと改めて実感しました。ぜひまたこうした場に参加したいと思います」と語った。

最後に、プロジェクト代表を務めるベネッセ教育総合研究所の小村俊平教育イノベーションセンター長は、次のように述べた。

「数学の定義を含めて、多様な角度から縦横無尽に対話し、思考を深められた場になりました。最後にお伝えしたいのは、なぜ日本では、18歳の時点で『総合的な数学力』が問われるのかといった疑問です。大学での専攻によって、必要とされる数学の分野は異なります。『この分野は好き』『これは役立ちそう』など、自分の興味・関心に応じて選んで学んでこそ、様々な気づきがあるはずです。『総合数学力』から『単元数学力』への転換が進むと、文系か理系かといった議論も不要になっていくのではないでしょうか。」